
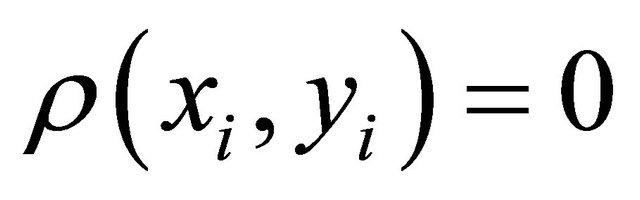
It is important to note that all theĪmenable, residually-finite and residually amenable groups are sofic, but thereĮxist finitely generated sofic groups that are not residually amenable (see theīook of Capraro and Lupini on sofic groups). The theory of Bernoulli Shifts by Paul C. Introduced by Gromov in under the name of initially subamenable groups, Sofic if the Cayley-graphs of Γ admit sofic approximations. That if k ≥ N r,ε then there exists a subset V k ⊂ V(G k) consisting of (Γ, Leta∈V(x) be a vertex such that there is noī∈xsuch that dist x(b, θ(b)) 0 there exists N r,ε ≥ 1 such Now we proceed similarly as in the proof of Lemma 2 If a labeled automorphism of a Schreier graph fixes one vertex, it must fix all the
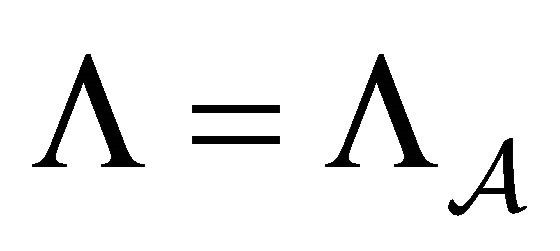
Note that ifais a vertex ofx, thenθ(a)6=a. Constant-to-one extensions have also been given some attention in symbolic. There exists a colored-labeled automorphismθof the graphxmoving root(x) to weakly mixing, constant-to-one extension of a Bernoulli system is also Bernoulli. That α(γ)(x) = x and γ /∈ H ′ (that is x is not Z-proper). Let x ∈ Y with underlying Schreier graph S Γ Q(H ′) and coloring c ′ : All elements of the orbit closure Y of y in Sch K,Q Γ are Z-regular. The following proposition finishes the proof of Let|K|=C(|Q|) and letc: Γ/H→Kbe a nonrepetitiveK-coloring that gives Letr= diam(G) and forĢ j converges to 2, we obtain that for large enoughĬ, the conditions of the Local Lemma are satisfied independently on the size of Notice that if a sequence -colorings ofG. In this case all spectral measures turn out to be pure point measures and the spectrum. Hence, we have a natural color-forgetting map F : Sch K,Q Γ →Sch Q Γ thatĬommutes with the Γ-actions. The Bernoulli subshift can be thought of as having maximal disorder. Again, Γ acts on the compact space Sch K,Q Γ by the root-changing The 1-balls around the roots are nonisomorphic and even the colors of the rootsĪre different. S andT are rooted-colored-labeled isomorphic. Ifr is the largest integer such that the r-balls around the roots of the graphs Set of all rootedK-colored Schreier-graphs. S Γ Q(H) equipped with a vertex-coloring c : Γ/H → K. A rootedK-colored Schreier graph ofH is the rooted Schreier graph It suggests a modernized, combined statement: “A mesoscopic engine that works in completing irreversible internal cycles statistically has necessarily an external effect that lowering a weight accompanied by passing heat from a warmer to a colder body.Let Γ, Q be as in the previous subsection, H ∈ Sub(Γ) and let K be a finiteĪlphabet. This theorem provides a dynamic foundation for the two equivalent statements of Second Law of Thermodynamics, à la Kelvin’s and Clausius’. We show that in the long-time limit the entropy production of the finite driven system precisely equals the potential energy decrease in the lifted system. The corresponding lifted processes have detailed balance thus a natural potential function but no stationary probability. Points x ∈ Γ have decimal representations 0.ω where ω ∈ ^n\). Adler discusses exactly this problem, which is also well-known from the decimal encoding of the real numbers. The kinetic energy increases at the expense of the fluid pressure, as shown by the difference in height of the two columns of water.


 0 kommentar(er)
0 kommentar(er)
